The Revised Universal Soil Loss Equation (RUSLE) is a widely used model designed to estimate long-term average annual soil loss caused by sheet and rill erosion from rainfall and associated overland flow. It’s especially valuable in land use planning, conservation practices, and watershed management.
RUSLE Formula:
A = R × K × LS × C × P
-
R FACTOR / Rainfall Erosivity Factor
The R factor quantifies the erosive force of rainfall based on the energy of raindrops and the rate of precipitation. It’s a key input in understanding how rainfall contributes to soil degradation.
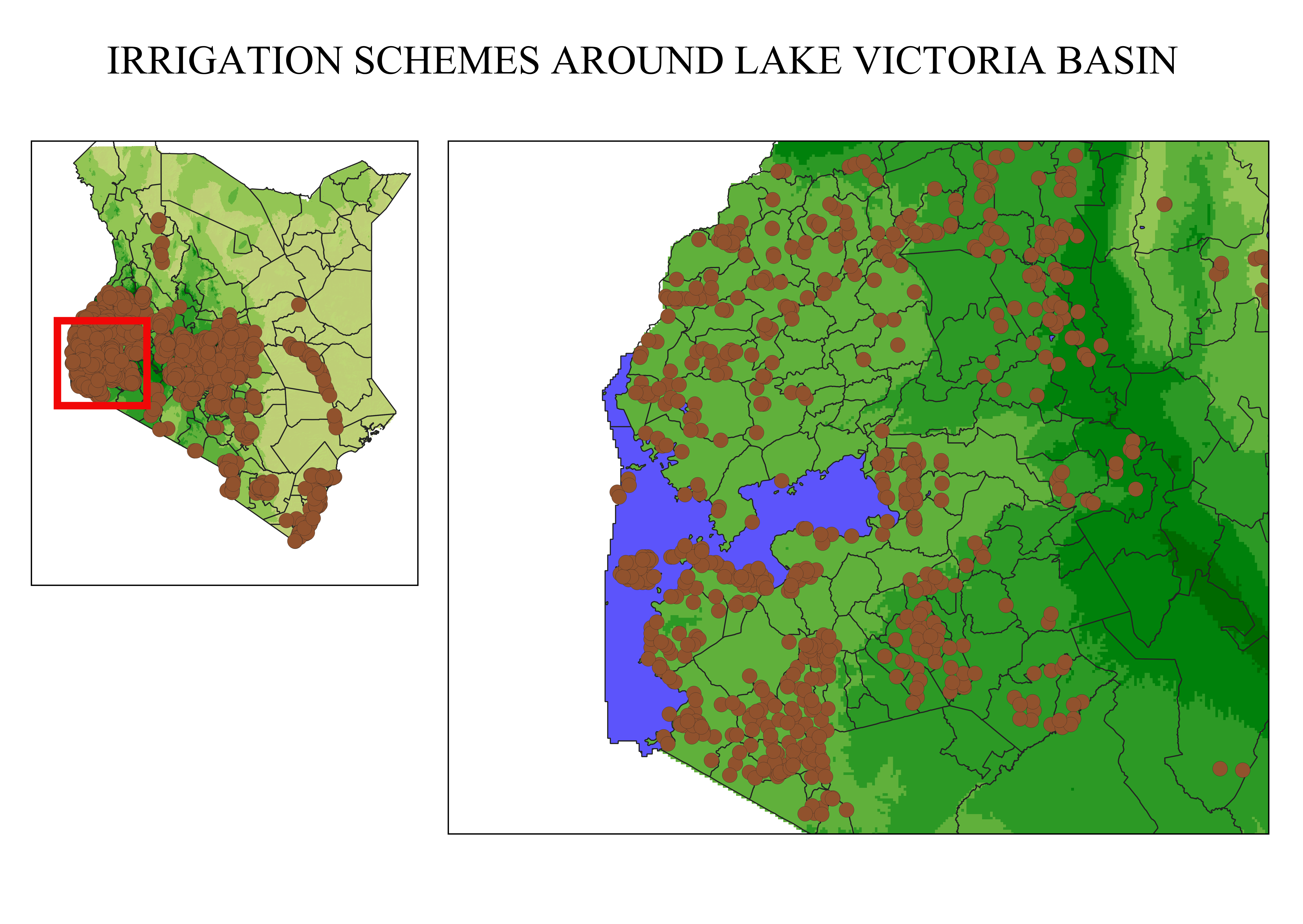
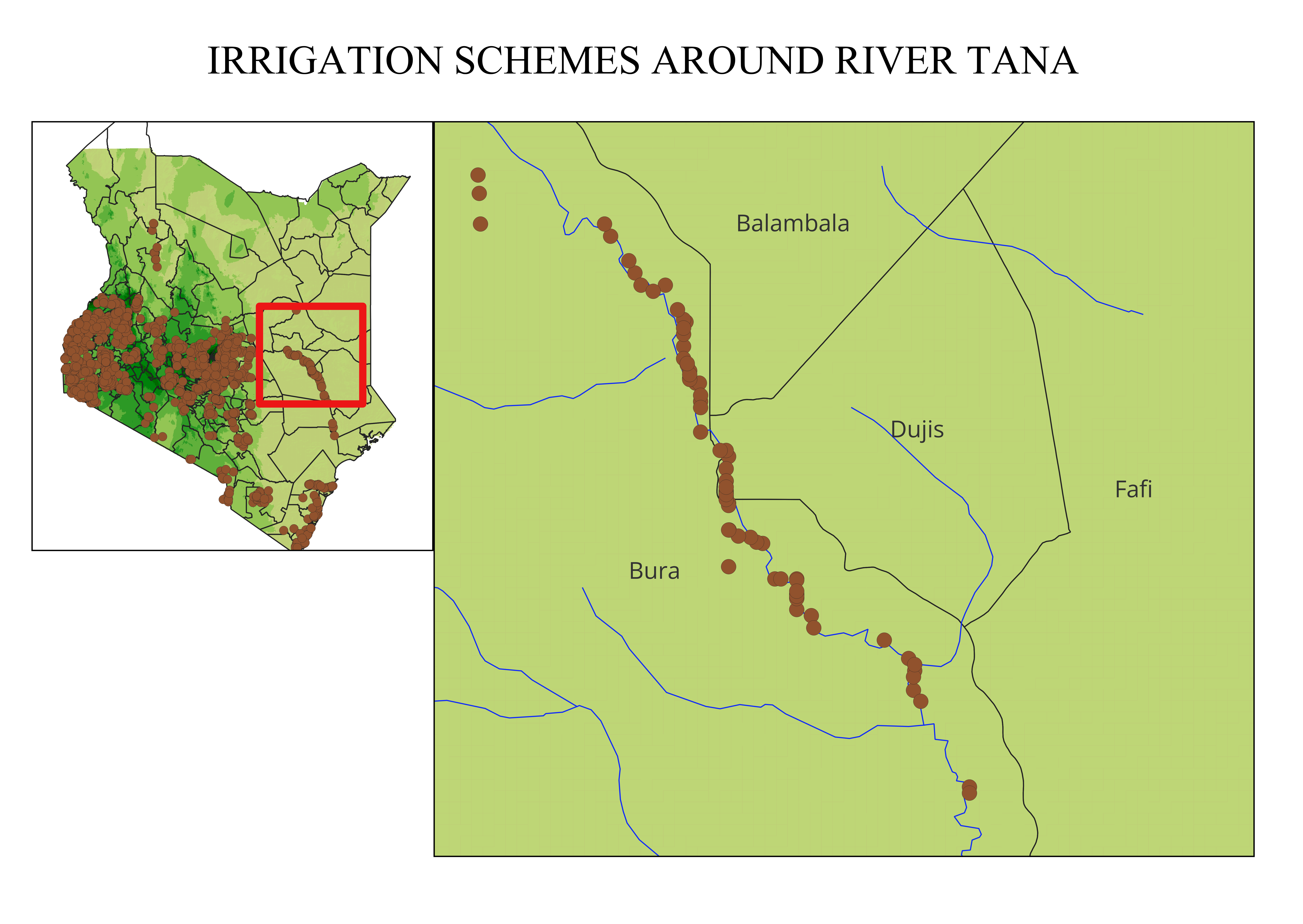
Data used: I used daily rainfall raster data for the year 2024 over the Machakos region, obtained from ClimateSERV. This platform provides satellite-based climate datasets suitable for spatial environmental analysis.
Method: Using Python, I aggregated daily rasters into a cumulative rainfall erosivity layer. Libraries like
rasterioandnumpyenabled efficient raster processing.Formula used: Since I lacked 30-minute interval rainfall data (I30), I applied the empirical formula:
R = ∑Pi²
Where Pi represents daily rainfall in millimeters. This empirical alternative is widely used in African contexts when high-resolution temporal data is unavailable.Why this formula: The original RUSLE model requires high-frequency data, which was not available. This empirical method provided a reliable and spatially consistent estimate using available daily data.
Alternative method – Kassam scenario: Some researchers apply monthly rainfall and interpolate values using IDW in QGIS, then apply empirical constants. Although viable, I focused on the daily raster approach for higher resolution and automation.
Comparison with KMD map: I validated the R-factor results by comparing with the Kenya Meteorological Department (KMD) erosivity maps. Despite KMD using station-based datasets, there were notable spatial similarities.
-
K FACTOR / Soil Erodibility Factor
The K factor describes the vulnerability of soil to erosion, influenced by its physical and chemical properties such as texture, organic matter, structure, and permeability.
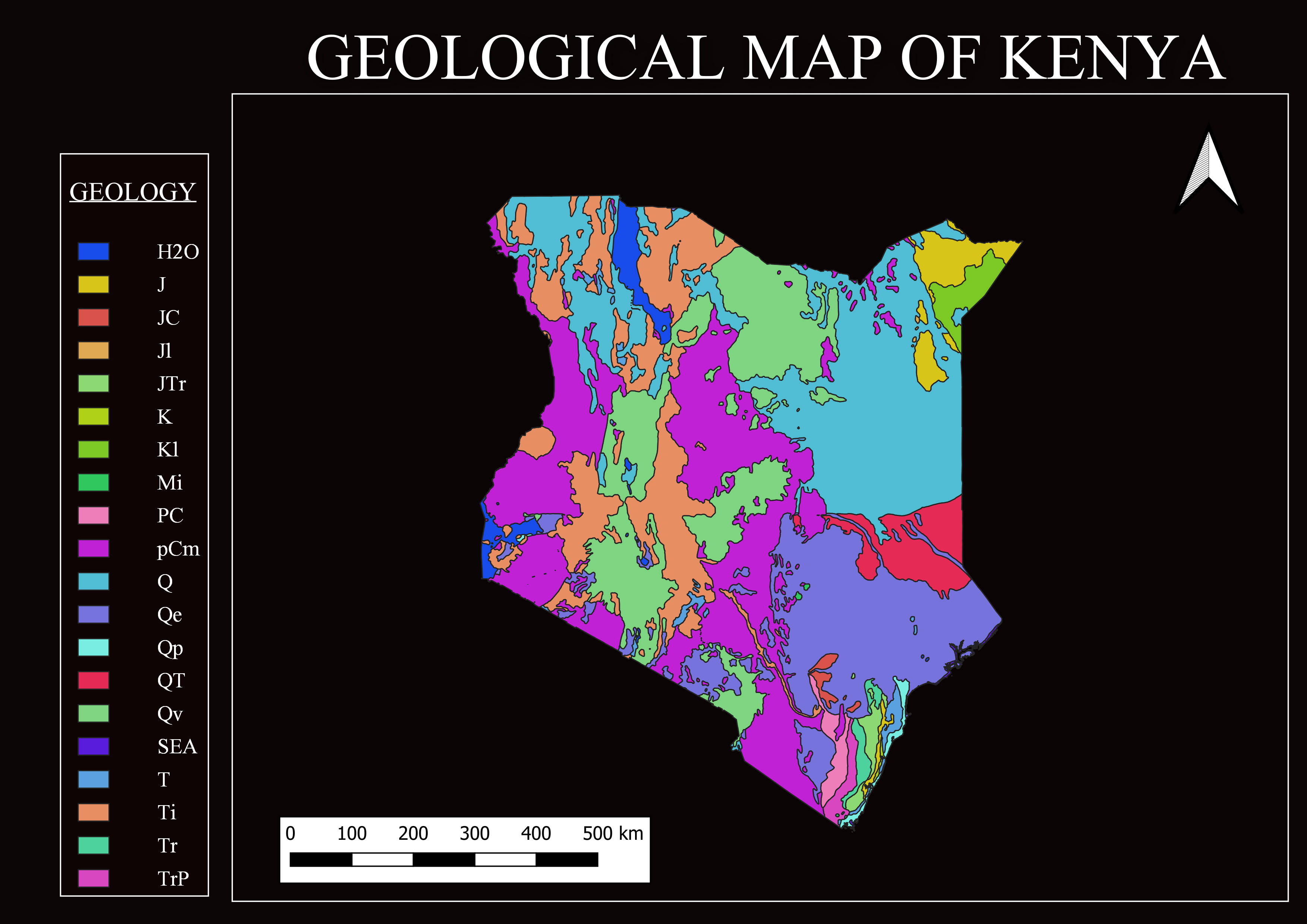
Data source: I used raster datasets from SoilGrids, which provide global coverage of soil properties in TIFF format suitable for GIS or Python-based analysis.
Formula applied: I adopted the Williams et al. (2000) equation:
K = fsand × fclay × forgC × fsilt × 0.1317
Each factor represents how a specific soil property contributes to erodibility:
- fsand: contribution of sand content
- fclay: influence of clay content
- forgC: role of organic carbon
- fsilt: impact of silt and textural balance
Why this method: I chose the Williams formula due to its compatibility with raster-based processing and its pixel-level estimation capabilities. The full coverage data from SoilGrids made this approach ideal.
Alternative approach – Kassam scenario: The Kassam method is generally used when data is collected from different field stations. K values are calculated at specific stations and interpolated (e.g., IDW) across the study area. This method suits field-sampled datasets but is less effective with raster data. Since my data was continuous and gridded, the raster-based method proved more efficient.
QGIS vs Python: While I initially attempted implementing the formula using QGIS's raster calculator, it proved cumbersome due to its limited formula flexibility. Python offered better control and efficiency for large raster datasets.
-
LS FACTOR / Slope Length and Steepness Factor
The LS factor in the RUSLE model quantifies the impact of topography — specifically slope length and steepness — on soil erosion. It reflects how water accumulates and flows over a landscape, gaining erosive power as slope and contributing area increase.
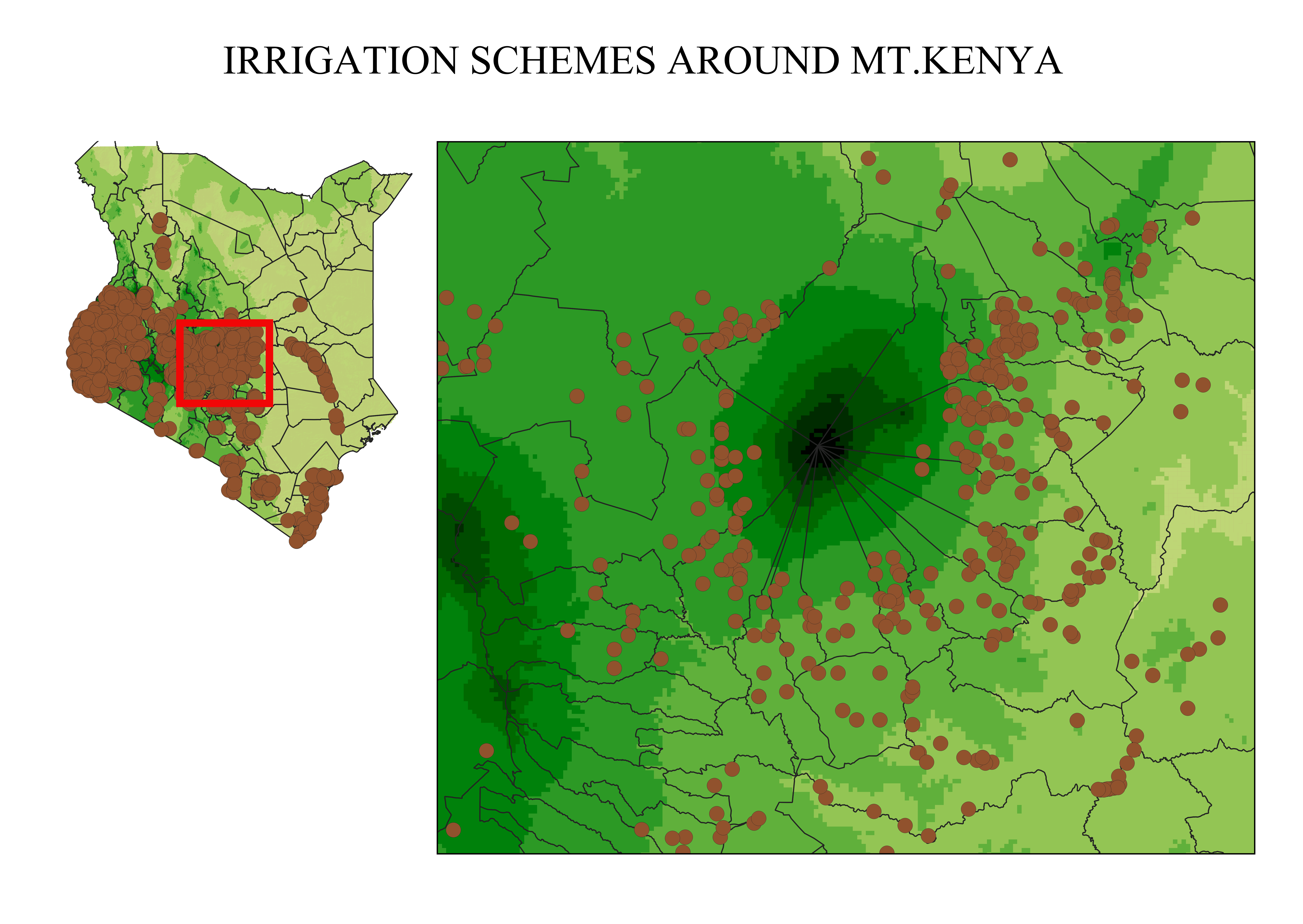
Data source used: I derived the LS factor using a Digital Elevation Model (DEM) with a resolution of 30 meters. From this DEM, I generated slope, flow direction, and flow accumulation rasters.
Formula applied: I used the Moore and Burch (1986) equation, which is widely adopted for pixel-based LS factor estimation:
LS = ((FlowAcc × CellSize) / 22.13)m × (sin(Slope) / 0.0896)n
- FlowAcc: Flow accumulation raster (number of upslope contributing cells)
- CellSize: Spatial resolution of DEM (e.g., 30m)
- Slope: Terrain slope in degrees (converted to radians for the sine function)
- m: Exponent typically between 0.4 and 0.6 depending on land characteristics (I used 0.4)
- n: Slope exponent, commonly 1.3
Software used: I implemented the LS factor calculation in Python using raster processing libraries for better control over mathematical operations and to automate the pixel-wise computation. Although QGIS can perform this analysis (especially using SAGA or GRASS tools like “LS Factor” or “Slope Length and Steepness”), I preferred Python for its reproducibility and flexibility in adjusting parameters.
Alternative using QGIS: The LS factor can also be calculated entirely within QGIS without writing code. This is done by using SAGA or GRASS GIS toolsets integrated into QGIS. The typical steps include:
- Filling sinks in the DEM using SAGA > Fill Sinks (Wang & Liu).
- Generating a Flow Accumulation raster using SAGA > Flow Accumulation (Top-Down).
- Calculating the slope using QGIS > Raster > Analysis > Slope or SAGA > Slope, Aspect, Curvature.
- Finally, computing the LS factor using SAGA > LS Factor tool, which directly applies the Moore and Burch (1986) method.
Note: The LS factor is essential in erosion modeling as it amplifies the soil loss based on terrain characteristics. Areas with long, steep slopes will have a higher LS value, indicating greater erosion potential.
-
C FACTOR / Cover Management Factor
The C Factor in the RUSLE model represents the effect of vegetation and land cover on soil erosion rates. It reflects the degree to which land cover—such as grass, shrubs, cropland, or built-up areas—protects the soil from the erosive power of rainfall and surface runoff.
Approach used: I computed the C Factor by assigning values to each land cover class based on the Dynamic World classification from Google Earth Engine. Each class (e.g., water, cropland, grassland, etc.) was mapped to a corresponding C Factor value ranging from 0 (no erosion risk) to 1 (maximum erosion risk).
Code Implementation: I wrote a Python script using
rasterioandnumpyto map LULC values to corresponding C Factor values and export the result as a raster. The script reads the LULC GeoTIFF, replaces each pixel value based on a predefined dictionary, and writes the new raster file to disk.Mapping of Dynamic World LULC codes to C values:
- Water (0) → 0.0
- Trees (1) → 0.002
- Grass (2) → 0.025
- Cropland (3) → 0.75
- Shrub & Scrub (4) → 0.125
- Built Area (5) → 0.0
- Bare Ground (6) → 1.0
- Snow & Ice (7) → 0.0
- Clouds (8) → 0.0
Validation and comparison: I verified the assigned values by inspecting individual areas in QGIS. The assigned C Factor values from Python matched those seen when manually inspecting the raster in QGIS, ensuring consistency across platforms.
Documentation and supporting studies: While I used class-based assignment rather than NDVI, it’s important to note that many studies use NDVI to estimate the C Factor due to its dynamic representation of vegetation. For example, the study by Benjamin K. Kogo(2020) on Western Kenya explains that:
“The C-factor accounts for the contribution of land cover towards soil loss and is thus an essential and dynamic element of the RUSLE model. The Normalized Difference Vegetation Index (NDVI) is used to estimate the C-factor because of its dynamic nature. The C-factor has an inverse relationship with NDVI and was computed using the equation:
C = exp[-a × (NDVI / (β − NDVI))]
where a = 2 and β = 1.”Why not NDVI? I chose not to use NDVI because the Dynamic World land cover classification already captures detailed land use information suitable for estimating the C Factor. This also avoided the need for complex satellite image preprocessing.
Software used: The computation was done in Python for automation and reproducibility. I also cross-verified the output in QGIS using the Identify Features tool to check the C values of different areas such as cropland, built-up, grassland, and bare ground.
Conclusion: The C Factor plays a crucial role in RUSLE modeling. Its accurate estimation ensures that vegetation’s protective role is well captured. In this analysis, both automated (Python) and manual (QGIS) checks confirmed the reliability of the generated C Factor raster.